What Is A Mixed Number In Math? Understanding The Basics And Beyond
Let’s dive into the world of mixed numbers, a concept you might have come across in math class but never fully grasped. Whether you're a student trying to ace your math exam or just someone curious about how numbers work, this article will break it down for you. Mixed numbers are more than just a fancy term; they’re a practical way to express quantities that are part whole and part fraction. So, buckle up, because we’re about to make math fun and easy to digest.
Now, before we jump into the nitty-gritty, let’s take a moment to appreciate how cool math is. Think about it—math is like a universal language that helps us understand the world around us. From baking a cake to building skyscrapers, math plays a role in almost everything. And mixed numbers? They’re one of the building blocks that make this language work.
But why should you care about mixed numbers? Well, understanding them can make your life easier. Imagine splitting a pizza with friends or calculating how much paint you need for a room. These real-world scenarios often involve mixed numbers, and knowing how to work with them can save you time and headaches. So, let’s get started and make sense of this math concept once and for all!
Defining Mixed Numbers in Math
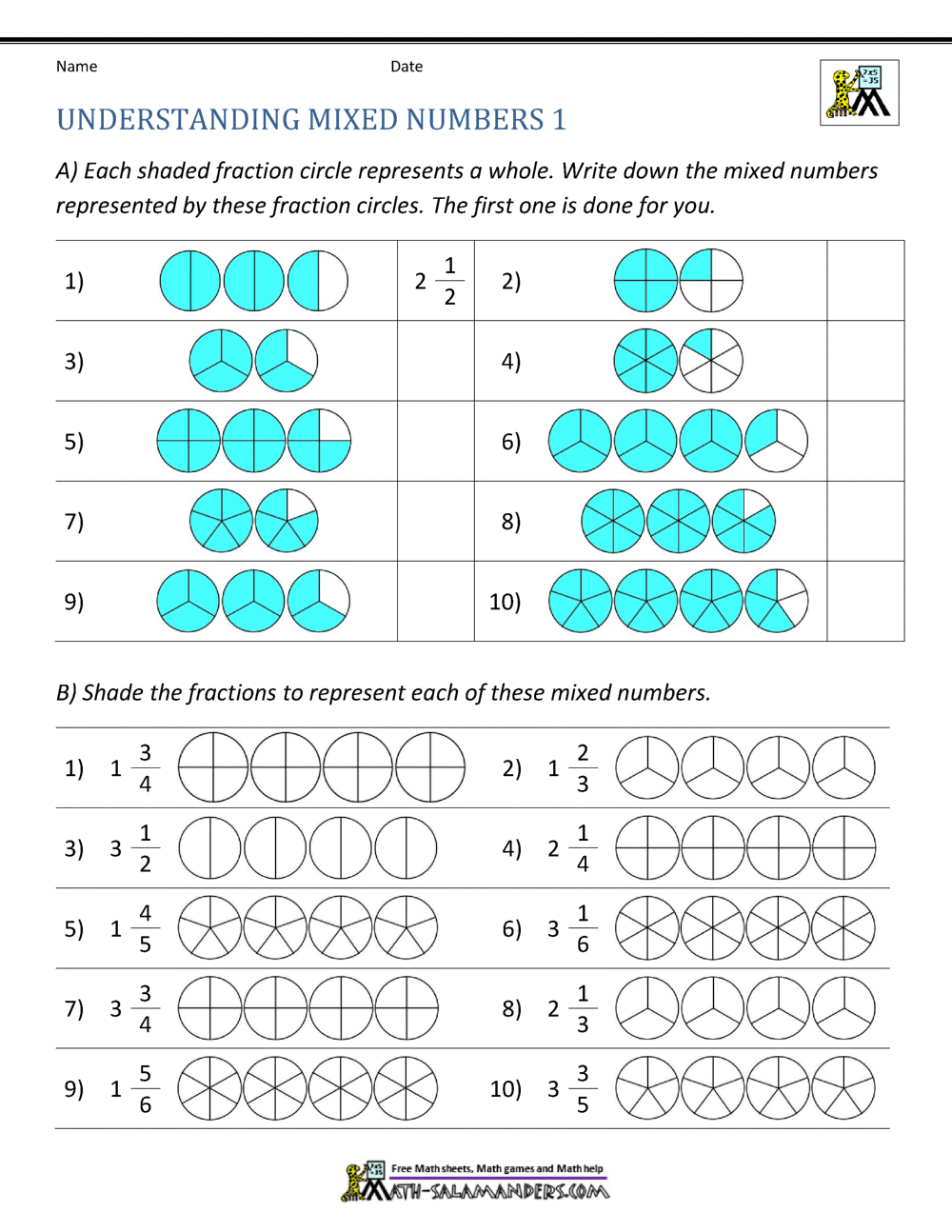
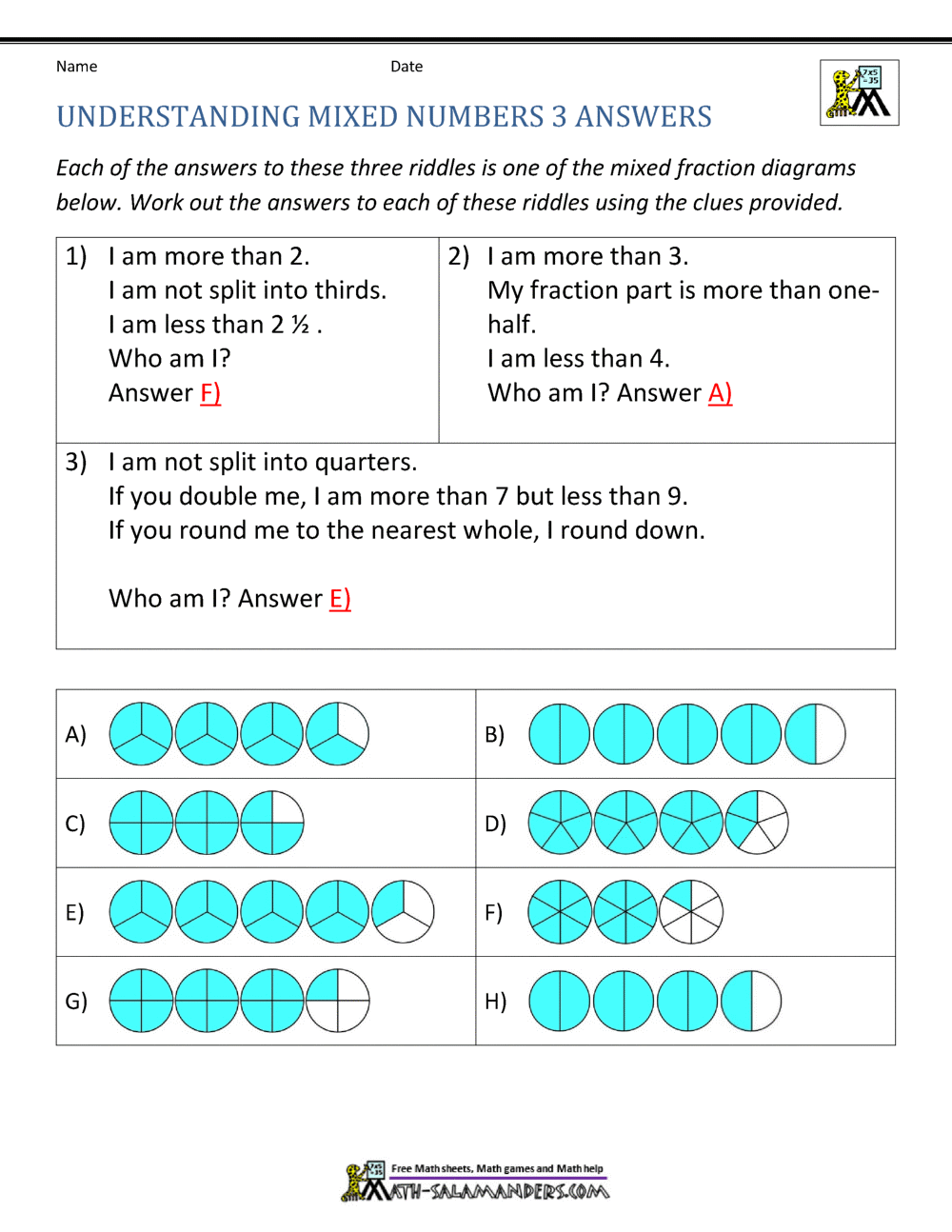
Alright, let’s get straight to the point. A mixed number is basically a combination of a whole number and a fraction. It’s like having a sandwich with a side of chips—both parts are important, but they serve different purposes. For example, if you see "2 1/2," that’s a mixed number. It means you have two whole units and an additional half unit.
Here’s the official definition: A mixed number consists of an integer (the whole number part) and a proper fraction (the fractional part). The proper fraction is always less than 1, which keeps things balanced. This format is super handy when you’re dealing with quantities that aren’t whole numbers but aren’t quite fractions either.
To visualize it, imagine cutting a cake into equal slices. If you eat three whole slices and half of another slice, you’ve consumed "3 1/2" slices. That’s a mixed number in action!
Why Mixed Numbers Matter
Let’s be real—mixed numbers aren’t just some abstract concept in a textbook. They have practical applications in everyday life. Whether you’re measuring ingredients for a recipe, calculating distances, or even dividing up resources, mixed numbers come in handy. Think about construction workers figuring out how much material they need or chefs scaling recipes for larger groups. Mixed numbers simplify these calculations and make them more manageable.
But there’s more to it than just practicality. Mixed numbers also help bridge the gap between whole numbers and fractions. They’re like the middle child of the math family, bringing together two important concepts into one neat package. By understanding mixed numbers, you’ll gain a deeper appreciation for how numbers interact and relate to each other.
Breaking Down Mixed Numbers
Whole Number vs. Fractional Part
When you look at a mixed number, the first thing you notice is the whole number. This is the integer part that represents complete units. For example, in "4 3/4," the whole number is 4. It tells you how many full units you have.
Then there’s the fractional part, which represents the "extra" or the incomplete unit. In our example, the fractional part is 3/4. This tells you how much of the next unit you have. Together, they form the mixed number "4 3/4," which means you have four full units and three-quarters of another unit.
It’s important to note that the fractional part is always a proper fraction, meaning the numerator (top number) is smaller than the denominator (bottom number). This ensures that the mixed number stays balanced and makes sense mathematically.
Converting Mixed Numbers to Improper Fractions
Sometimes, it’s easier to work with improper fractions instead of mixed numbers. An improper fraction is when the numerator is greater than or equal to the denominator. To convert a mixed number to an improper fraction, follow these steps:
- Multiply the whole number by the denominator of the fraction.
- Add the numerator to the result from step 1.
- Write the sum as the new numerator, keeping the original denominator.
For example, let’s convert "2 1/3" to an improper fraction:
- 2 × 3 = 6
- 6 + 1 = 7
- The improper fraction is 7/3.
This conversion is especially useful when you’re doing operations like addition, subtraction, multiplication, or division with mixed numbers.
Adding and Subtracting Mixed Numbers
Adding Mixed Numbers
Adding mixed numbers might seem tricky at first, but it’s actually pretty straightforward. Here’s how you do it:
- Separate the whole numbers and fractions.
- Add the whole numbers together.
- Add the fractions together (make sure they have the same denominator).
- Combine the results and simplify if necessary.
For example, let’s add "1 1/4" and "2 3/4":
- Whole numbers: 1 + 2 = 3
- Fractions: 1/4 + 3/4 = 4/4 = 1
- Combine: 3 + 1 = 4
So, "1 1/4 + 2 3/4 = 4."
Subtracting Mixed Numbers
Subtracting mixed numbers works similarly to addition, but you need to be careful when the fractional part of the minuend (the number being subtracted from) is smaller than the fractional part of the subtrahend (the number being subtracted). In such cases, you’ll need to borrow from the whole number part. Here’s an example:
- Subtract "2 1/3" from "3 2/3."
- Whole numbers: 3 - 2 = 1
- Fractions: 2/3 - 1/3 = 1/3
- Combine: 1 + 1/3 = 1 1/3
So, "3 2/3 - 2 1/3 = 1 1/3."
Multiplying and Dividing Mixed Numbers
Multiplication and division of mixed numbers are a bit different from addition and subtraction. The key is to convert the mixed numbers into improper fractions first. Here’s how it works:
Multiplying Mixed Numbers
- Convert both mixed numbers to improper fractions.
- Multiply the numerators together and the denominators together.
- Simplify the result if necessary and convert back to a mixed number if needed.
For example, let’s multiply "1 1/2" and "2 1/3":
- Convert: 1 1/2 = 3/2, 2 1/3 = 7/3
- Multiply: (3 × 7) / (2 × 3) = 21/6
- Simplify: 21/6 = 3 3/6 = 3 1/2
Dividing Mixed Numbers
- Convert both mixed numbers to improper fractions.
- Flip the second fraction (find its reciprocal) and multiply.
- Simplify the result and convert back to a mixed number if needed.
For example, let’s divide "2 1/2" by "1 1/3":
- Convert: 2 1/2 = 5/2, 1 1/3 = 4/3
- Divide: (5/2) ÷ (4/3) = (5/2) × (3/4) = 15/8
- Simplify: 15/8 = 1 7/8
Real-World Applications of Mixed Numbers
Now that you’ve got the basics down, let’s talk about how mixed numbers apply to real life. Whether you’re cooking, crafting, or even budgeting, mixed numbers pop up all the time. Here are a few examples:
- Cooking: Recipes often call for measurements like "1 1/2 cups of flour" or "2 1/4 teaspoons of sugar."
- Construction: Builders use mixed numbers to measure materials, such as "4 3/8 inches of wood."
- Time Management: You might schedule a meeting for "2 1/2 hours" or plan a trip that takes "5 3/4 days."
By understanding mixed numbers, you’ll be better equipped to tackle these everyday challenges with confidence.
Tips for Mastering Mixed Numbers
Learning about mixed numbers doesn’t have to be overwhelming. Here are some tips to help you master this concept:
- Practice regularly: The more you work with mixed numbers, the more comfortable you’ll become.
- Use visual aids: Draw diagrams or use manipulatives to help visualize the numbers.
- Break it down: Focus on one operation at a time (addition, subtraction, multiplication, division).
- Seek help: Don’t hesitate to ask your teacher, tutor, or classmates for clarification.
Remember, math is a skill that improves with practice. So, keep at it and don’t give up!
Common Mistakes to Avoid
Even the best math students make mistakes when working with mixed numbers. Here are a few common pitfalls to watch out for:
- Forgetting to simplify fractions: Always simplify your answers to their lowest terms.
- Incorrect borrowing: When subtracting, make sure you borrow correctly from the whole number part.
- Improper conversions: Double-check your conversions between mixed numbers and improper fractions.
By being aware of these mistakes, you’ll be less likely to fall into them. Practice makes perfect, so keep practicing until it becomes second nature.
Conclusion: Embrace the Power of Mixed Numbers
In summary, mixed numbers are an essential part of math that help us express quantities that are part whole and part fraction. They’re practical, versatile, and incredibly useful in everyday life. By understanding how to define, convert, and operate with mixed numbers, you’ll gain a valuable skill that will serve you well in many situations.
So, what’s next? Take what you’ve learned and put it into practice. Try solving some problems on your own or challenge yourself with real-world scenarios. And don’t forget to share this article with friends or classmates who might find it helpful. Together, let’s make math fun and accessible for everyone!
Table of Contents:
- Defining Mixed Numbers in Math
- Why Mixed Numbers Matter
- Breaking Down Mixed Numbers
- Converting Mixed Numbers to Improper Fractions
- Adding and Subtracting Mixed Numbers
- Multiplying and Dividing Mixed Numbers
- Real-World Applications of Mixed Numbers
- Tips for Mastering Mixed Numbers
- Common Mistakes to Avoid
- Conclusion: Embrace the Power of Mixed Numbers